Geometría : Memo
Fórmulas para calcular los perímetros
El perímetro de una figura cerrada se define como la longitud de su contorno.
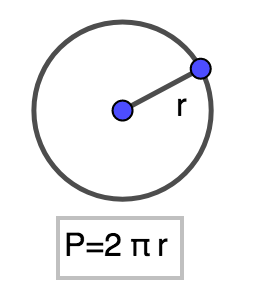
Perímetro de un círculo
La fórmula para calcular el perímetro de un círculo es `P=2*pi*r`, donde r es el radio del círculo.
Ejemplo: el
perímetro de un círculo de longitud 1 es igual a 2*pi
.
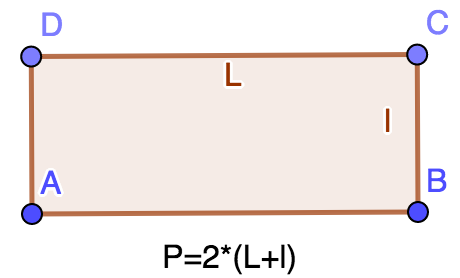
Perímetro de un rectángulo
El perímetro de un rectángulo viene dado por la fórmula `2*(L+l)` donde L es la longitud y l la anchura de un lado.
Aplicando esta fórmula, se puede comprobar que el
perímetro de un rectángulo de longitud 3 y anchura 2 es igual a 10
.
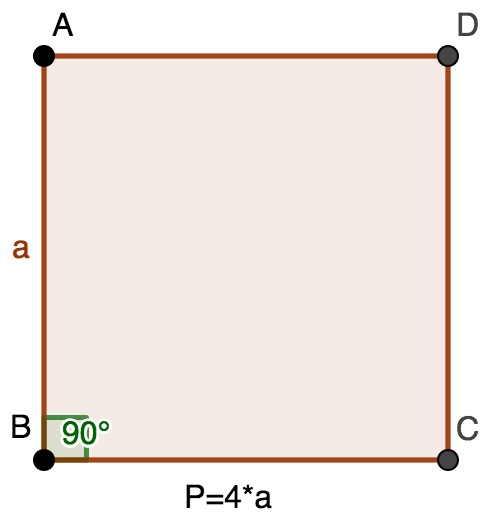
Perímetro de un cuadrado
El perímetro de un cuadrado viene dado por la fórmula `4*a` donde a es la longitud de un lado del cuadrado.
Utilizando esta fórmula, podemos demostrar que el
perímetro de un cuadrado de longitud 2 es igual a 8
.
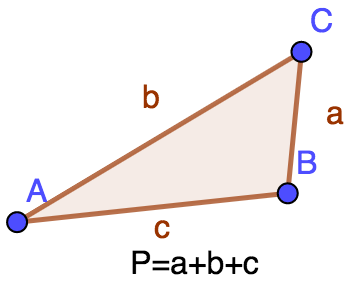
Perímetro de un triángulo
El perímetro de un triángulo viene dado por la fórmula a+b+c, donde a, b y c son la longitud de cada lado del triángulo.
Usando esta fórmula, podemos ver que el
perímetro de un triángulo con lados de longitud 5, 6, 7 es 18
.
Fórmulas de superficie
Área de un círculo
El área de un círculo viene dada por la fórmula `pi*r^2`, donde r es el radio del círculo.
Aplicando esta fórmula, es posible encontrar el área de un círculo de radio 3.
Área de un rectángulo
El área de un rectángulo es igual al producto de sus lados y se calcula mediante la fórmula `(L*l)`, donde L es la longitud y l la anchura de un lado. Utilizando esta fórmula, podemos comprobar que la longitud es 3 y la anchura es 6.
Área de un cuadrado
El área de un cuadrado viene dada por la fórmula `a^2`, donde a es la longitud de un lado del cuadrado.
Con esta fórmula podemos, por ejemplo, calcular el área de un cuadrado cuya longitud de lado es 3.
Área de un triángulo
El área de un triángulo puede calcularse mediante la fórmula de Herón, que se escribe: `S=sqrt(p*(p-a)*(p-b)*(p-c)`, donde a, b, c son las longitudes de los lados del triángulo, y p es la mitad del perímetro `p=(a+b+c)/2`.
Con esta fórmula podemos, por ejemplo, calcular el área de un triángulo cuyas longitudes de los lados son 3, 4 y 5 respectivamente .
Fórmulas de cálculo de volúmenes
Volumen de una esfera (bola)
El volumen de una esfera viene dado por la fórmula `4/3*pi*r^3`, donde r representa el radio de la esfera. Esta fórmula permite, por ejemplo, calcular el volumen de una esfera de radio 3 .
Volumen de un paralelepípedo rectangular
El volumen de un paralelepípedo rectangular viene dado por la fórmula `(L*l*h)`, donde L es la longitud, l es la anchura de un lado y h es la altura. Con esta fórmula podemos calcular el volumen de un paralelepípedo rectangular cuya longitud es 3, la anchura es 2 y la altura es 4 .
Volumen de un cubo
El volumen de un cubo viene dado por la fórmula `l^3`, donde l es la longitud de un lado. Aplicando esta fórmula, es posible encontrar el volumen de un cubo que tiene lados de longitud 3.
Teorema de Pitágoras
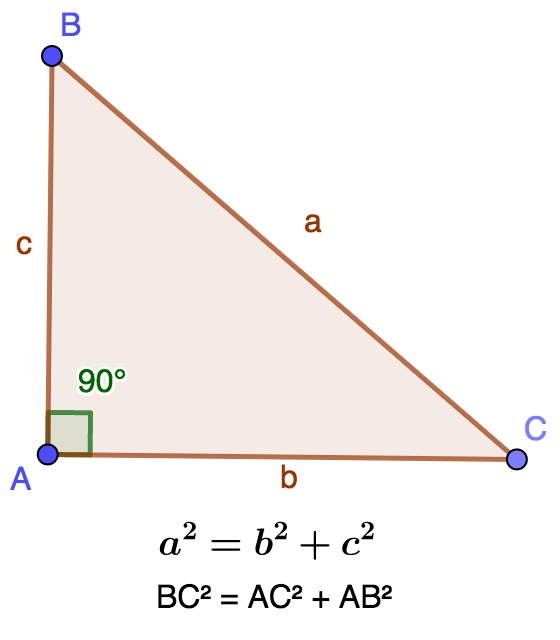
El teorema de Pitágoras se enuncia como sigue : En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los lados opuestos.
Si consideramos el triángulo ABC rectangular en A, si ponemos BC=a, AC=b, AB=c entonces el teorema de Pitágoras se escribe
`BC^2=AB^2+AC^2` o `a^2=b^2+c^2`.
El teorema de Pitágoras tiene un recíproco que se enuncia así: Si en un triángulo el cuadrado de un lado es igual a la suma de los cuadrados de los lados opuestos, entonces el triángulo es rectangular.
Aplicando el teorema de Pitágoras, es posible, por ejemplo, calcular la longitud de la hipotenusa de un triángulo rectángulo cuyos lados adyacentes tienen longitudes de 3 y 4.