Geometry : Reminder
Formulas for calculating perimeters
The perimeter of a closed figure is defined as the length of its contour.
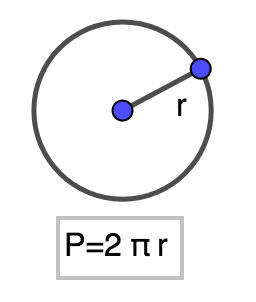
Perimeter of a circle
The formula for calculating the perimeter of a circle is `P=2*pi*r`, where r is the radius of the circle.
Example : the perimeter of a circle of length 1 is equal to 2*pi.
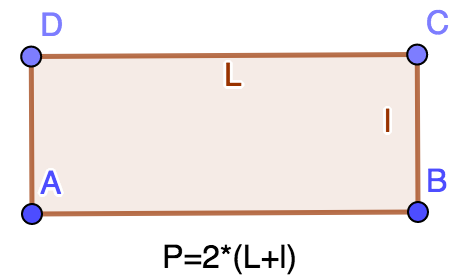
Perimeter of a rectangle
The perimeter of a rectangle is given by the formula `2*(L+l)` where L represents the length and l the width of a side.
Applying this formula, it is possible to verify that the
perimeter of a rectangle of length is 3 and width is 2 is equal to 10
.
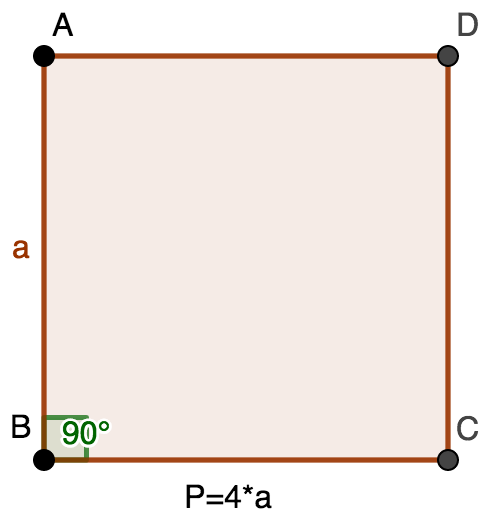
Perimeter of a square
The perimeter of a square is given by the formula `4*a` where a is the length of one side of the square.
Using this formula, we can show that the
perimeter of a square of length 2 equals 8
.
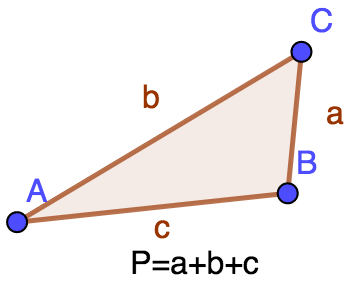
Perimeter of a triangle
The perimeter of a triangle is given by the formula a+b+c
where a, b, and c represent the length of each side of the triangle.
Using this formula, we can see that the
perimeter of a triangle whose sides have lengths 5, 6, 7 is equal to 18
.
Formulas for calculating areas
Area of a circle
The area of a circle is given by the formula `pi*r^2`, where r represents the radius of the circle.
By applying this formula, it is possible to find the area of a circle of radius 3 .
Area of a rectangle
The area of a rectangle is equal to the product of its sides, it is calculated with the formula `(L*l)`, where L represents the length and l the width of a side. Using this formula, we can verify that the length is 3 and the width is equal to 6 .
Area of a square
The area of a square is given by the formula `a^2` where a represents the length of one side of the square.
Using this formula, we can, for example, calculate the area of a square whose side length is 3.
Area of a triangle
The area of a triangle can be calculated using Heron's formula , which is written: `S=sqrt(p*(p-a)*(p-b)*(p-c)`, where a, b, c represent the length of the sides of the triangle, and p is the half perimeter `p=(a+b+c)/2`.
Using this formula, we can, for example, calculate the area of a triangle of a triangle where the length of each of the sides would be 3, 4, and 5 respectively.
Formulas for calculating volumes
Volume of a sphere (ball)
The volume of a sphere is given by the formula `4/3*pi*r^3`, where r represents the radius of the sphere. For example, this formula can be used to calculate the volume of a sphere of radius 3.
Volume of a rectangular parallelepiped
The volume of a rectangular parallelepiped is given by the formula `(L*l*h)`, where L represents the length, l the width of a side, and h the height. Using this formula, we can calculate the volume of a rectangular parallelepiped whose length is 3, width is 2, and height is 4 .
Volume of a cube
The volume of a cube is given by the formula `l^3`, where l is the length of a side. By applying this formula, it is possible to find the volume of a cube that has sides of length 3 .
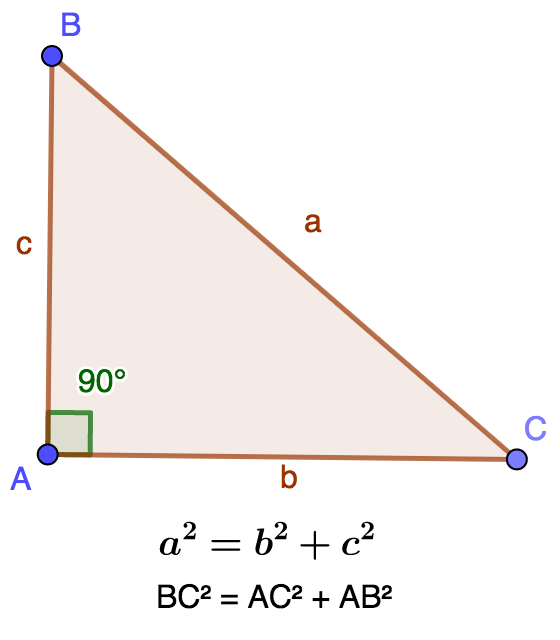
Pythagorean Theorem
The Pythagorean theorem is stated as follows :
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the opposite sides.
If we consider the triangle ABC rectangular in A, if we pose BC=a, AC=b, AB=c then the Pythagorean theorem is written
`BC^2=AB^2+AC^2` or `a^2=b^2+c^2`.
The Pythagorean theorem admits a reciprocal which states: If in a triangle the square of one side is equal to the sum of the squares of the opposite sides, then the triangle is rectangular.
By applying the Pythagorean theorem, it is for example possible to calculate the length of the hypotenuse of a right-angled triangle whose adjacent sides have lengths of 3 and 4 .