Satz des Pythagoras Rechnung : Wie benutzt man es?
Der Rechner für rechtwinklige Dreiecke verwendet den Satz des Pythagoras, um zu überprüfen, ob ein Dreieck rechtwinklig ist, oder um die Länge einer Seite eines rechtwinkligen Dreiecks zu ermitteln.
Syntax :
pythagoras(länge_angrenzende_seite;länge_angrenzende_seite;hypotenuse_länge)
Beispiele :
- pythagoras(`3;4;5`) 1 liefert
- pythagoras(`3;4;x`) 5 liefert
Rechtwinkliges-Dreieck-Rechner
Der Taschenrechner mit der pythagoras-Funktion ermöglicht es zu wissen, ob die Längen den Satz von Pythagoras bestätigen. Wenn die Längen Variablen enthalten, versucht der Rechner, die Werte der Variablen zu finden, die es ermöglichen, den Satz von Pythagoras zu überprüfen.
Der Satz von Pythagoras wird wie folgt ausgedrückt:
In einem rechteckigen Dreieck ist das Quadrat der Hypotenuse gleich der Summe der Quadrate auf gegenüberliegenden Seiten.
Wenn wir das rechteckige Dreieck in A: ABC betrachten, wenn wir BC=a, AC=b, AB=c setzen, dann wird der Satz des Pythagoras geschrieben:
`BC^2=AB^2+AC^2` oder `a^2=b^2+c^2`.
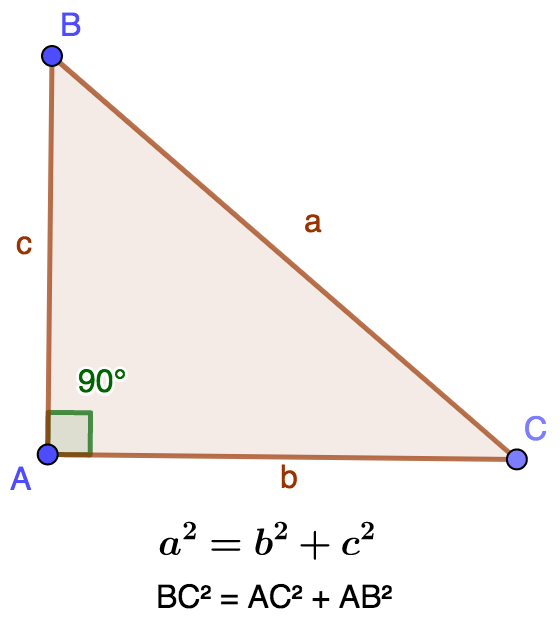
Das Satz des Pythagoras gibt einen Gegenwert zu, der wie folgt ausgedrückt wird: Wenn in einem Dreieck das Quadrat auf einer Seite gleich der Summe der Quadrate auf den gegenüberliegenden Seiten ist, dann ist das Dreieck ein Dreieckrechteckig.
Überprüfen Sie, ob ein Dreieck ein Rechteck ist, das die Länge seiner Seiten kennt
Der Rechner überprüft, ob ein Dreieck ein rechteckiges Dreieck ist, ausgehend von der Länge der Hypotenuse und der Länge der gegenüberliegenden Seiten. Wenn Sie beispielsweise überprüfen möchten, ob es ein rechteckiges Dreieck gibt, dessen Hypotenuse eine Länge von 5 und die gegenüberliegenden Seiten eine Länge von 3 und 4 haben, müssen Sie eingeben: pythagoras(`3;4;5`). Der Taschenrechner gibt 1 zurück, wenn die im Parameter übergebenen Werte den Schluss zulassen, dass das Dreieck ein Rechteck ist, andernfalls 0. Der Taschenrechner gibt die Details der Berechnungen zurück, die zur Verwendung des Satzes des Pythagoras verwendet wurden.
Die Länge einer Seite eines rechtwinkligen Dreiecks aus der Länge der anderen beiden Seiten ermitteln
Der Taschenrechner ermöglicht es, die Länge einer Seite zu bestimmen, wenn man die beiden anderen Seiten kennt, indem man den Satz des Pythagoras anwendet. Auf diese Weise kann man die Länge der Hypotenuse oder die Länge einer der Seiten, die an den rechten Winkel angrenzen, berechnen.
Suchen Sie die Länge der Hypotenuse
Mit dem Taschenrechner kann man die Länge der Hypotenuse finden, wenn man die Länge der an den rechten Winkel angrenzenden Seiten kennt. Wenn man zum Beispiel die Hypotenuse eines rechtwinkligen Dreiecks sucht, dessen benachbarte Seiten 3 und 4 betragen, muss man pythagoras(`3;4;x`) eingeben, der Wert der Hypotenuse wird dann errechnet.
Die Länge einer an den rechten Winkel angrenzenden Seite suchen
Mit dem Taschenrechner kann man die Länge einer an den rechten Winkel angrenzenden Seite ermitteln, wenn man die Länge der Hypotenuse und die Länge der anderen angrenzenden Seite kennt. Wenn man zum Beispiel die Länge der Seite eines rechtwinkligen Dreiecks sucht, deren Hypotenuse 5 und die Länge der anderen Seite 3 beträgt, muss man pythagoras(`x;3;5`) eingeben, dann wird der Wert der Seite, die an den rechten Winkel angrenzt, errechnet.
Es ist auch möglich, die Länge der Seiten eines rechtwinkligen, gleichschenkligen Dreiecks anhand der Länge der Hypotenuse zu ermitteln. Wenn man zum Beispiel die Länge der an den rechten Winkel angrenzenden Seiten eines gleichschenkligen rechtwinkligen Dreiecks mit der Hypotenuse 4 sucht, muss man pythagoras(`x;x;4`) eingeben.
Quiz zum Satz des Pythagoras
Um die Anwendung des Satzes des Pythagoras zu üben, bietet die Seite ein Anwendungsquiz an.
- Flächeninhalt eines Quadrats : flache_quadrats. Online-Flächenrechner, der die Flächeninhalt eines Quadrats aus einer Seitenlänge berechnet.
- Kreisfläche : kreisflache. Flächen-Online-Rechner, der die Fläche eines Kreises aus seinem Radius oder aus seinem Durchmesser berechnen kann.
- Flächeninhalt eines Rechtecks : flacheninhalt_rechteck. Der Online-Flächenrechner ermöglicht es Ihnen, die Flächeninhalt eines Rechtecks aus seiner Länge und Breite zu berechnen.
- Geradengleichung : geradengleichung. Der Geradengleichungsrechner berechnet die reduzierte Gleichung einer Geraden aus den Koordinaten zweier Punkte und gibt dabei die Rechenschritte an.
- Umfang Rechner : umfang. Online-Taschenrechner, der den Umfang eines Rechtecks, Quadrats, Dreiecks oder Kreises berechnet.
- Umfang eines Quadrats : umfang_quadrats. Online-Umkreisrechner, der den Umfang eines Quadrats von der Länge einer Seite aus berechnet.
- Umfang eines Kreises : umfang_kreises. Online-Perimeterrechner, der den Umfang eines Kreises aus seinem Radius berechnet.
- Umfang eines Rechtecks : umfang_rechtecks. Online-Perimeterrechner zum Berechnen des Umfangs eines Rechtecks aus seiner Länge und Breite.
- Satz des Pythagoras Rechnung : pythagoras. Der Rechner für rechtwinklige Dreiecke verwendet den Satz des Pythagoras, um zu überprüfen, ob ein Dreieck rechtwinklig ist, oder um die Länge einer Seite eines rechtwinkligen Dreiecks zu ermitteln.
- Berechnung der Fläche einer geometrischen Figur : flache. Online-Flächenrechner, der es ermöglicht, die Fläche eines Rechtecks, Quadrats, Dreiecks oder Kreises zu berechnen.
- Volumen eines Würfels : wurfel_volumen. Online-Volumenrechner, mit dem Sie das Volumen eines Würfels aus der Länge auf einer Seite berechnen können.
- Volumen eines Quaders : quader_volumen. Online-Volumenrechner, der das Volumen eines Rechtecks aus seiner Länge, Breite und Höhe berechnet.
- Volumen einer Kugel : kugel_volumen. Online-Volumenrechner, mit dem Sie das Volumen einer Kugel aus ihrem Radius berechnen können.