Théorème de Pythagore calculatrice : Comment l'utiliser ?
Le calculateur utilise le théorème de Pythagore pour vérifier qu'un triangle est rectangle ou trouver la longueur d'un coté d'un triangle rectangle.
Syntaxe :
pythagore(longueur_cote_adjacent;longueur_cote_adjacent;longueur_hypotenuse)
Exemples :
- pythagore(`3;4;5`) retourne 1
- pythagore(`3;4;x`) retourne 5
Théorème de Pythagore calcul en ligne
Le calculateur grâce à la fonction pythagore permet de savoir si des longueurs vérifient le théorème de Pythagore. Si les longueurs contiennent des variables le calculateur va chercher à trouver les valeurs des variables qui permettent de vérifier le théorème de Pythagore.
Le théorème de Pythagore s'énonce de la manière suivante : Dans un triangle rectangle, le carré de l’hypoténuse est égal
à la somme des carrés des cotés opposés.
Si on considère le triangle ABC rectangle en A, si on pose BC=a, AC=b, AB=c alors le théorème de Pythagore s'écrit
`BC^2=AB^2+AC^2` ou encore `a^2=b^2+c^2`.
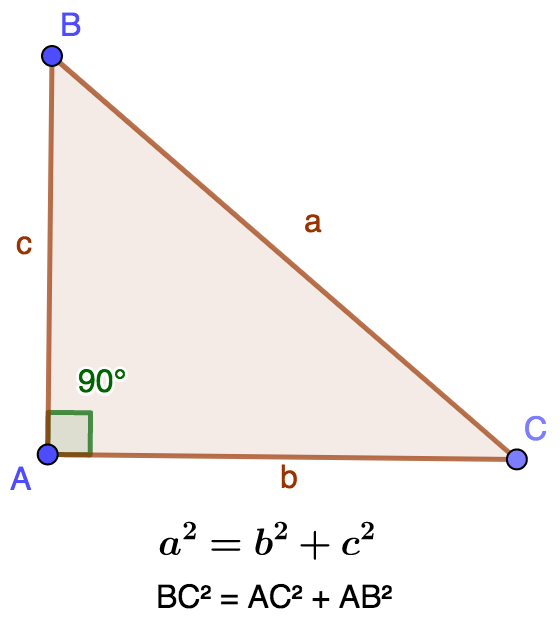
Le théorème de Pythagore admet une réciproque qui s'énonce ainsi : Si dans un triangle le carré d'un coté est égal à la somme des carrés des cotés opposés, alors le triangle est rectangle.
Vérifier qu'un triangle est rectangle connaissant la longueur de ses cotés
La calculatrice permet de vérifier qu'un triangle est rectangle à partir de la longueur de l'hypoténuse et de la longueur des cotés opposés. Si on souhaite par exemple vérifier qu'il existe un triangle rectangle dont l'hypoténuse aurait pour longueur 5 et les cotés opposés pour longueur 3 et 4, il faut saisir pythagore(`3;4;5`). La calculatrice retourne 1 si les valeurs passées en paramètre permettent d'en déduire que le triangle est rectangle, 0 sinon. La calculatrice retourne les détails des calculs permettant d'utiliser le théorème de Pythagore.
Trouver la longueur d'un coté d'un triangle rectangle à partir de la longueur des deux autres
La calculatrice permet de trouver la longueur d'un coté connaissant les deux autres grâce au théorème de pythagore, il est ainsi possible de calculer la longueur de l'hypoténuse ou la longueur d'un des cotés adjacents à l'angle droit.
Rechercher la longueur de l'hypoténuse
La calculatrice permet de trouver la longueur de l'hypoténuse si l'on connait la longueur des cotés adjacents à l'angle droit. Par exemple si on cherche l'hypoténuse d'un triangle rectangle dont les cotés adjacents valent 3 et 4, il faut saisir pythagore(`3;4;x`), la valeur de l'hypoténuse est alors calculé.
Rechercher la longueur d'un coté adjacent à l'angle droit
La calculatrice permet de trouver la longueur d'un coté adjacent à l'angle droit si l'on connait la longueur de l'hypoténuse et la longueur de l'autre coté adjacent. Par exemple si on cherche la longueur du coté d'un triangle rectangle dont l'hypoténuse vaut 5 et la longueur de l'autre coté vaut 3,il faut saisir pythagore(`x;3;5`), la valeur du coté adjacent à l'angle droit est alors calculé.
Il est aussi possible de trouver la longueur des cotés d'un triangle rectangle isocèle à partir de longueur de l'hypoténuse. Par exemple si l'on cherche la longueur des cotés adjacents à l'angle droit d'un triangle rectangle isocèle qui a pour hypoténuse 4, il faut saisir pythagore(`x;x;4`).
Quiz et exercice sur le théorème de Pythagore
Le site propose des quiz et un exercice sur le théorème de Pythagore, cet exercice de géométrie est corrigé et propose une application concrète de l'utilisation du théorème.
- Aire d'un carré : aire_carre. Calculateur d'aire en ligne qui permet de calculer l'aire d'un carré à partir de la longueur d'un coté.
- Aire d'un cercle : aire_cercle. Calculateur d'aire en ligne qui permet de calculer l'aire d'un cercle à partir de son rayon ou de son diamètre.
- Aire d'un rectangle : aire_rectangle. Calculateur d'aire en ligne permet de calculer l'aire d'un rectangle à partir de sa longueur et de sa largeur.
- Déterminer une équation de droite à partir de deux points : equation_droite. Le calculateur d'équation de droite calcule l'équation réduite d'une droite à partir des coordonnées de deux points en précisant les étapes de calcul.
- Calculatrice de périmètres : perimetre. Calculateur de périmètre en ligne qui permet de calculer le périmètre d'un rectangle, d'un carré, d'un triangle ou d'un cercle.
- Périmètre d'un carré : perimetre_carre. Calculateur de périmètre en ligne qui permet de calculer le périmètre d'un carré à partir de la longueur d'un coté.
- Périmètre d'un cercle : perimetre_cercle. Calculateur de périmètre en ligne qui permet de calculer le périmètre d'un cercle à partir de son rayon.
- Périmètre d'un rectangle : perimetre_rectangle. Calculateur de périmètre en ligne de calculer le périmètre d'un rectangle à partir de sa longueur et de sa largeur.
- Théorème de Pythagore calculatrice : pythagore. Le calculateur utilise le théorème de Pythagore pour vérifier qu'un triangle est rectangle ou trouver la longueur d'un coté d'un triangle rectangle.
- Calcul de la surface d'une figure géométrique : surface. Calculateur de surface en ligne qui permet de calculer la surface d'un rectangle, d'un carré, d'un triangle ou d'un cercle.
- Volume d'un cube : volume_cube. Calculateur de volume en ligne qui permet de calculer le volume d'un cube à partir de la longueur d'un coté.
- Volume d'un parallélépipède rectangle : volume_rectangle. Calculateur de volume en ligne qui permet de calculer le volume d'un rectangle à partir de sa longueur, de sa largeur et de sa hauteur.
- Volume d'une sphère : volume_sphere. Calculateur de volume en ligne qui permet de calculer le volume d'une sphère à partir de son rayon.