A calculadora do triângulo direito usa o teorema de Pitágoras para verificar se um triângulo está em ângulo reto ou para encontrar o comprimento de um lado de um triângulo em ângulo reto.

Calculadora triangular direita (Teorema de Pitágoras)

LA calculadora graças à função pitagoras possibilita saber se comprimentos verificam o teorema de Pitágoras. Se os comprimentos contiverem variáveis, a calculadora procurará encontrar os valores das variáveis, que permitem verificar o teorema de Pitágoras.

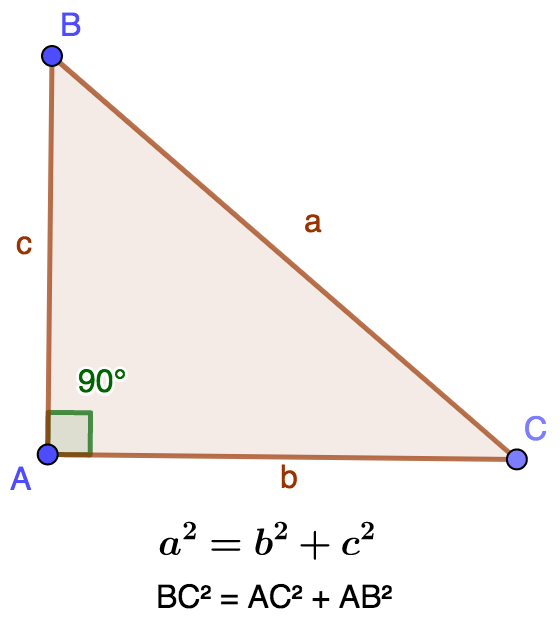
O teorema de Pitágoras é declarado da seguinte maneira : Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos lados opostos. Se considerarmos o triângulo retângulo ABC em A, se colocarmos BC=a, AC=b, AB=c então o teorema de Pitágoras é escrito `BC^2=AB^2+AC^2` ou `a^2=b^2+c^2`.

O teorema de Pitágoras admite uma recíproca que é expressa da seguinte forma : Se num triângulo o quadrado de um lado é igual à soma dos quadrados dos lados opostos, então o triângulo é retângulo.

Verifique se um triângulo é retângulo, conhecendo o comprimento de seus lados

A calculadora torna possível verificar se um triângulo é retângulo a partir do comprimento da hipotenusa e o comprimento dos lados opostos. Se se deseja, por exemplo, verificar que existe um triângulo retângulo cuja hipotenusa teria comprimento 5 e lados opostos para comprimento 3 e 4, é necessário entrar pitagoras(`3;4;5`). A calculadora retorna 1 se os valores passados no parâmetro permitem deduzir que o triângulo é retângulo, 0 caso contrário. A calculadora retorna os detalhes dos cálculos, tornando possível usar o teorema de Pitágoras.

Encontrar o comprimento de um lado de um triângulo em ângulo recto a partir do comprimento dos outros dois

A calculadora permite que você encontre o comprimento de um lado conhecendo os outros dois lados graças ao teorema de Pitágoras, assim é possível calcular o comprimento da hipotenusa ou o comprimento de um dos lados adjacentes ao ângulo reto.

Encontrar o comprimento de um lado adjacente ao ângulo reto

A calculadora permite que você encontre o comprimento de um lado adjacente ao ângulo reto se você souber o comprimento da hipotenusa e o comprimento do outro lado adjacente. Por exemplo, se você estiver procurando o comprimento do lado de um triângulo em ângulo reto cuja hipotenusa é 5 e o comprimento do outro lado é 3, você precisa entrar pitagoras(`3;4;x`), o valor do lado adjacente ao ângulo reto é então calculado.

Encontrar o comprimento de um lado adjacente ao ângulo reto

A calculadora permite que você encontre o comprimento de um lado adjacente ao ângulo reto se você souber o comprimento da hipotenusa e o comprimento do outro lado adjacente. Por exemplo, se você estiver procurando o comprimento do lado de um triângulo em ângulo reto cuja hipotenusa é 5 e o comprimento do outro lado é 3, você precisa entrar pitagoras(`x;3;5`), o valor do lado adjacente ao ângulo reto é então calculado.

Também é possível encontrar o comprimento dos lados de um triângulo isósceles direito a partir do comprimento da hipotenusa. Por exemplo, se você estiver procurando o comprimento dos lados adjacentes ao ângulo reto de um triângulo isósceles direito cuja hipotenusa é 4, você entraria em pitagoras(`x;x;4`).

Quiz sobre o teorema de Pitágoras

Para praticar o uso do teorema de Pitágoras, o site oferece um quiz de aplicação.

Sintaxe :

pitagoras(comprimento lado adjacente;comprimento lado adjacente; comprimento de hipotenusa)

Exemplos :

• pitagoras(`3;4;5`) retorna 1
• pitagoras(`3;4;x`) retorna 5