Mental Calculation Games: Focus on Subtraction
This page offers a variety of mental calculation games that allow children to practice arithmetic operations, especially subtractions. The games are designed to help students master the basic math skills required in the English National Curriculum.
For example, the "Four Operations Game" allows students to revise addition, subtraction, multiplication, and division, which aligns with the skills expected in Key Stages 1 and 2. The "Missing Sign Game" helps children choose the correct arithmetic operator, reinforcing their understanding of basic operations and their ability to solve problems, as outlined in the Key Stage 1 and 2 objectives.
The "Number Crunching Game" focuses on quick calculations with whole numbers, a key skill for students in Key Stages 1 and 2. The "Three Operations Game" and the "Missing Number Game" offer additional exercises to revise and deepen skills in addition, subtraction, and multiplication, which are essential for learning math in Key Stages 1 and 2.
Finally, the "Magic Squares Game" allows children to practice completing a number grid to form a magic square, where the sum of the numbers in each row, column, and diagonal is the same. The "Subtraction Tables Game" allows for learning and practicing subtractions with small whole numbers, promoting mental calculation practice from Key Stage 1 onwards. These games are effective educational tools to support students in their math learning by offering regular and enjoyable practice of arithmetic operations.
Missing number game (subtraction)
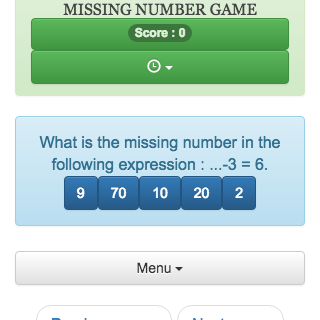 Online calculation game: You must find the missing number in a mathematical expression.
Online calculation game: You must find the missing number in a mathematical expression.
Missing operator game (subtraction)
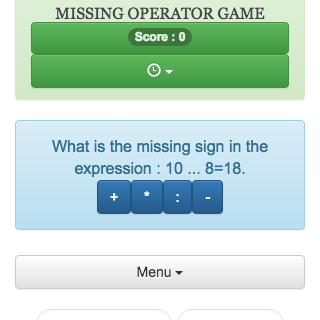 Online calculation game consisting of finding the missing operator in a mathematical expression.
Online calculation game consisting of finding the missing operator in a mathematical expression.
Four operations game (subtraction)
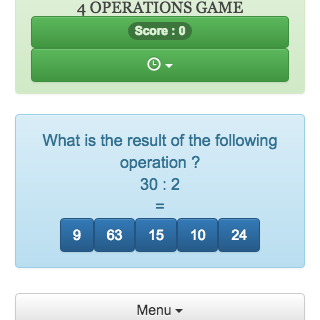 This online game of mental calculation, allows to revise addition, subtraction, multiplication and division, It helps students in learning arithmetic operations.
This online game of mental calculation, allows to revise addition, subtraction, multiplication and division, It helps students in learning arithmetic operations.
Countdown game (subtraction)
 The goal of the countdown maths game is to find a target number using arithmetic operations from a list of given numbers.
The goal of the countdown maths game is to find a target number using arithmetic operations from a list of given numbers.
Three operations game (subtraction)
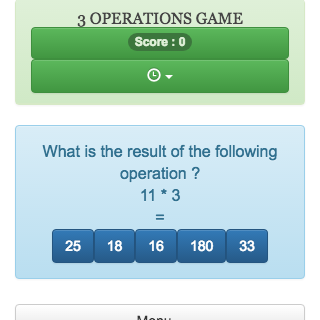 Online mental calculation game, allows to review addition, subtraction and multiplication, this game helps students to practise arithmetic operations.
Online mental calculation game, allows to review addition, subtraction and multiplication, this game helps students to practise arithmetic operations.
Magic square game (subtraction)
 The goal of the game is to complete a magic square that has empty areas.
The goal of the game is to complete a magic square that has empty areas.
Subtraction tables game (subtraction)
 Online mental calculation game to help to memorize the subtraction tables.
Online mental calculation game to help to memorize the subtraction tables.
- 1st 2nd 3rd Grade
- 2nd Grade
- 3rd Grade
- 4th 5th 6th Grade
- 4th Grade
- 5th Grade
- 6th Grade
- 7 year old
- 7th Grade
- 8 year old
- 8th Grade
- 9 year old
- 9th Grade
- 10 year old
- 11 year old
- 12 year old
- 13 year old
- 14 year old
- 15 year old
- addition
- division
- educational games
- elementary school
- freshman year
- games and quizzes corrected
- games for kids
- junior
- mental calculation
- Middle School
- multiplication
- numbers
- numerical calculation
- subtraction
- year 10