Pythagorean theorem calculator : How to use it?
The calculator uses the Pythagorean theorem to verify that a triangle is right-angled or to find the length of one side of a right-angled triangle.
Syntax :
pythagorean(length_adjacent_side;length_adjacent_side;hypotenuse_length)
Examples :
- pythagorean(`3;4;5`) returns 1
- pythagorean(`3;4;x`) returns 5
Pythagorean theorem online calculator
The calculator by means of the pythagorean function makes it possible to know if lengths satisfy the Pythagorean theorem. If the lengths contain variables, the calculator will seek to find the values of the variables which allow to verify the Pythagorean theorem.
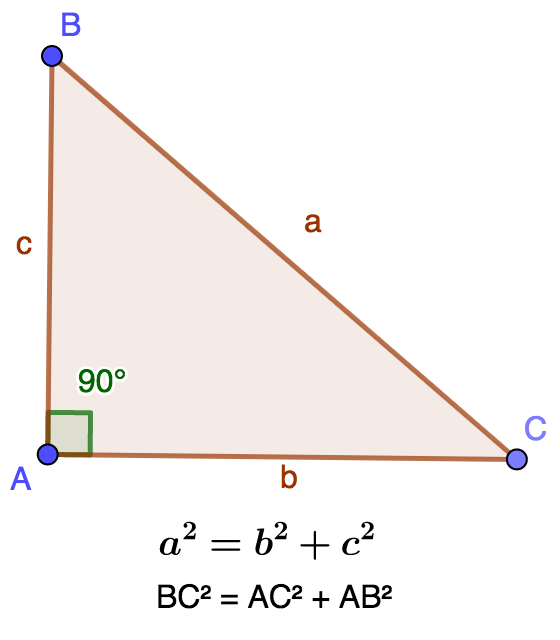
The Pythagorean theorem is expressed as follows: In a right triangle, the square of the hypotenuse is equal to the sum of
the squares of the opposite sides. If we consider the triangle ABC rectangle in A, if we put BC = a, AC = b, AB = c then
the theorem of Pythagoras is written
`BC^2=AB^2+AC^2` or `a^2=b^2+c^2`.
The Pythagorean theorem admits a reciprocal which states : If in a triangle the square of one side is equal to the sum of the squares of the opposite sides, then the triangle is a right triangle.
Verify that a triangle is a right triangle knowing the length of its sides
The calculator makes it possible to verify that a triangle is a right triangle knowing the length of the hypotenuse and the length of the opposite sides. If it is desired, for example, to verify that there exists a right-angled triangle whose hypotenuse has length 5 and the opposite sides for length 3 and 4, enter pythagorean(`3;4;5`). The calculator returns 1 if the values passed in parameter make it possible to deduce that the triangle is a right triangle, 0 otherwise. The calculator returns the details of the calculations used to use the Pythagorean theorem.
Find the length of one side of a right triangle from the length of the other two
The calculator allows you to find the length of one side knowing the two others thanks to the Pythagorean theorem. It is thus possible to calculate the length of the hypotenuse or the length of one of the sides adjacent to the right angle.
Find the length of the hypotenuse
The calculator allows to find the length of the hypotenuse if we know the length of the sides adjacent to the right angle. For example, if you are looking for the hypotenuse of a right-angled triangle whose adjacent sides are 3 and 4, you need to enter pythagorean(`3;4;x`), the value of the hypotenuse is then calculated.
Find the length of a side adjacent to the right angle
The calculator allows to find the length of a side adjacent to the right angle if we know the length of the hypotenuse and the length of the other adjacent side. For example, if you are looking for the length of the side of a right-angled triangle whose hypotenuse is 5 and the length of the other side is 3, you need to enter pythagorean(`x;3;5`), the value of the side adjacent to the right angle is then calculated.
It is also possible to find the length of the sides of an isosceles right triangle from the length of the hypotenuse. For example, if you are looking for the length of the sides adjacent to the right angle of an isosceles right triangle whose hypotenuse is 4, you must enter pythagorean(`x;x;4`).
Quiz on the Pythagorean theorem
In order to practice using the Pythagorean theorem, the site offers an application quiz.
- Area of a square : area_square. Area online calculator that can calculate the area of a square from the length of a side.
- Area of a circle : area_circle. Area online calculator that can calculate the area of a circle from its radius or from its diameter.
- Area of a rectangle : area_rectangle. Area online calculator that can calculate the area of a rectangle from its length and its width.
- Find equation of a straight line from two points : equation_straight_line. The equation straight line calculator allows to calculate the equation of a straight line from the coordinates of two points with step by step calculation.
- Perimeter calculator : perimeter. Online perimeter calculator that calculates rectangle perimeter, square perimeter, triangle perimeter or circle perimeter.
- Perimeter of a square : perimeter_square. The online calculator allows to calculate the perimeter of a square from the length of a side.
- Perimeter of a circle : perimeter_circle. Online calculator that calculates the perimeter of a circle from its radius.
- Perimeter of a rectangle : perimeter_rectangle. The online calculator allows to calculate the perimeter of a rectangle from its length and its width.
- Pythagorean theorem calculator : pythagorean. The calculator uses the Pythagorean theorem to verify that a triangle is right-angled or to find the length of one side of a right-angled triangle.
- Calculation of the area of a geometric figure. : area. Online area calculator which allows to calculate the area of a rectangle, square, triangle or circle.
- Volume of a cube : volume_cube. The online calculator allows to calculate the volume of a cube from the length of a side.
- Volume of a rectangular parallelepiped : volume_rectangle. The online calculator allows to calculate the volume of a rectangle from its length, its width and height.
- Volume of a sphere : volume_sphere. The online calculator allows to calculate the volume of a sphere from its radius.